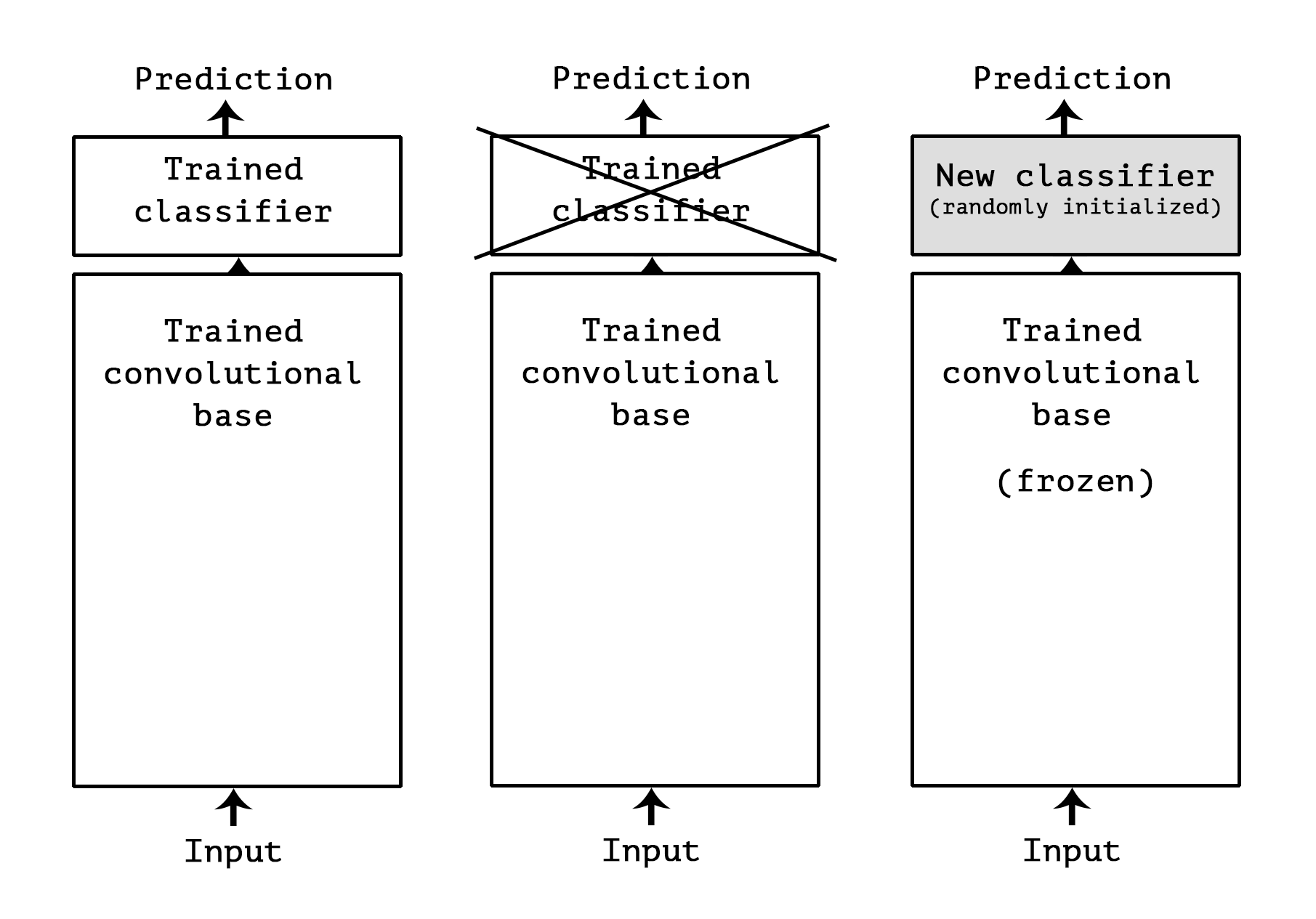
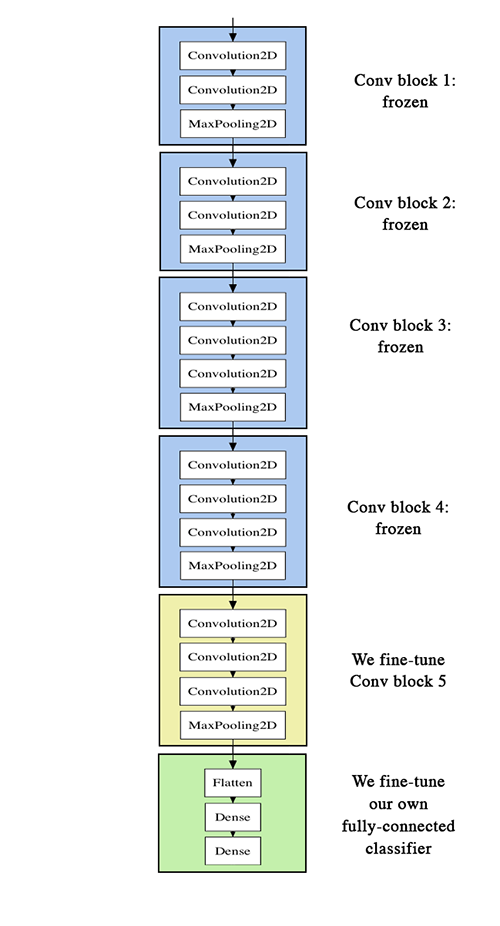
Model: "vgg16"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 150, 150, 3)] 0
_________________________________________________________________
block1_conv1 (Conv2D) (None, 150, 150, 64) 1792
_________________________________________________________________
block1_conv2 (Conv2D) (None, 150, 150, 64) 36928
_________________________________________________________________
block1_pool (MaxPooling2D) (None, 75, 75, 64) 0
_________________________________________________________________
block2_conv1 (Conv2D) (None, 75, 75, 128) 73856
_________________________________________________________________
block2_conv2 (Conv2D) (None, 75, 75, 128) 147584
_________________________________________________________________
block2_pool (MaxPooling2D) (None, 37, 37, 128) 0
_________________________________________________________________
block3_conv1 (Conv2D) (None, 37, 37, 256) 295168
_________________________________________________________________
block3_conv2 (Conv2D) (None, 37, 37, 256) 590080
_________________________________________________________________
block3_conv3 (Conv2D) (None, 37, 37, 256) 590080
_________________________________________________________________
block3_pool (MaxPooling2D) (None, 18, 18, 256) 0
_________________________________________________________________
block4_conv1 (Conv2D) (None, 18, 18, 512) 1180160
_________________________________________________________________
block4_conv2 (Conv2D) (None, 18, 18, 512) 2359808
_________________________________________________________________
block4_conv3 (Conv2D) (None, 18, 18, 512) 2359808
_________________________________________________________________
block4_pool (MaxPooling2D) (None, 9, 9, 512) 0
_________________________________________________________________
block5_conv1 (Conv2D) (None, 9, 9, 512) 2359808
_________________________________________________________________
block5_conv2 (Conv2D) (None, 9, 9, 512) 2359808
_________________________________________________________________
block5_conv3 (Conv2D) (None, 9, 9, 512) 2359808
_________________________________________________________________
block5_pool (MaxPooling2D) (None, 4, 4, 512) 0
=================================================================
Total params: 14,714,688
Trainable params: 14,714,688
Non-trainable params: 0
_________________________________________________________________